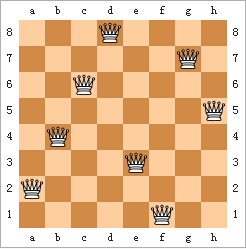
八皇后问题是一个以国际象棋为背景的问题：如何能够在8×8的国际象棋棋盘上放置八个皇后，使得任何一个皇后都无法直接吃掉其他的皇后？

为了达到此目的，任两个皇后都不能处于同一条横行、纵行或斜线上。(皇后在米字形方向上通吃)

八皇后问题可以推广为更一般的n皇后摆放问题：这时棋盘的大小变为n×n，而皇后个数也变成n。当且仅当n = 1或n ≥ 4时问题有解。

八皇后问题最早是由国际国际象棋棋手马克斯·贝瑟尔于1848年提出。之后陆续有数学家对其进行研究，其中包括高斯和康托，并且将其推广为更一般的n皇后摆放问题。八皇后问题的第一个解是在1850年由弗朗兹·诺克给出的。诺克也是首先将问题推广到更一般的n皇后摆放问题的人之一。1874年，S.冈德尔提出了一个通过行列式来求解的方法，这个方法后来又被J.W.L.格莱舍加以改进。

八皇后问题一共有92个互不相同的解。如果将旋转和对称的解归为一种的话，则一共有12个独立解。

8皇后php代码如下：

<?php

define('BR', nl2br(PHP_EOL));
$queen = array();//各皇后所在的位置  array($row=>$col,...)
$cont = 0;//统计解得个数

//获取输入的n
$n = ($n = intval($_GET['n'])) ? $n : 8;

if ($n > 20) {
    echo "n值太大，不能求解!" . BR;
} else {
    echo "{$n}皇后问题求解如下:" . BR;
    placeQueen(1);        //问题从最初状态,第1行解起
}

/**
 * 输出结果
 * @global array $queen 皇后位置数组
 * @global int $n 皇后个数
 * @global int $cont 第几个解
 */
function printResult() {
    global $queen;
    global $n;
    global $cont;

    $cont++;
    echo "第{$cont}个解：";
    for ($i = 1; $i <= $n; $i++)
        echo "({$i},{$queen[$i]}) ";

    echo BR;
    for ($row = 1; $row <= $n; $row++) {        //行
        for ($col = 1; $col <= $n; $col++) {    //列
            if ($queen[$row] != $col)
                echo "O ";
            else
                echo "X ";
        }
        echo BR;
    }
}

/**
 * 检验第row行的col列上是否可以安全的摆放皇后
 * @global array $queen 皇后位置数组
 * @param int $row 行
 * @param int $col 列
 * @return boolean 是否安全
 */
function isSafe($row, $col) {
    global $queen;
    $tmpRow = 1;
    
    //tmpRow=1到row-1是已经放置了皇后的行
    while ($tmpRow < $row) {
        if(!isset($queen[$tmpRow])){
            return true;
        }
        
        //第tmpRow行的皇后是否在col列 或 (tmpRow,qeen[col])与(row,col)是否在斜线上
        if ($queen[$tmpRow] == $col || abs($tmpRow - $row) == abs($queen[$tmpRow] - $col)){
            return false;
        }
        $tmpRow++;
    }
    return true;
}

/**
 * 放置皇后
 * @global array $queen 皇后位置数组
 * @global int $n 皇后个数
 * @param int $row 第几行
 */
function placeQueen($row) {
    global $queen;
    global $n;

    if ($row > $n)
        printResult();
    else {
        //试探第row行的每一个列
        for ($col = 1; $col <= $n; $col++) {
            if (isSafe($row, $col)) {
                $queen[$row] = $col;
                //继续放置row+1行
                placeQueen($row + 1);
            }
        }
    }
}

结果输出：

8皇后问题求解如下:
第1个解：(1,1) (2,5) (3,8) (4,6) (5,3) (6,7) (7,2) (8,4) 
X O O O O O O O 
O O O O X O O O 
O O O O O O O X 
O O O O O X O O 
O O X O O O O O 
O O O O O O X O 
O X O O O O O O 
O O O X O O O O 
第2个解：(1,1) (2,6) (3,8) (4,3) (5,7) (6,4) (7,2) (8,5) 
。。。。。。
。。。